LRU 缓存题目

程序员面试有一个比较经典的题目：leetcode-144-LRU缓存（Least Recently Used）。

简单描述一下题目，有几个要点：

1. 缓存初始化时设置一个容量 capacity。当缓存容量达到上限时，移除最久未使用的键值对。
2. get(key)：如果缓存中存在键 key，则返回其对应的值，否则返回 -1。
3. put(key, value)：如果键 key 已存在，则更新其值；如果键 key 不存在，则插入该键值对。
4. 函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

处理这种场景的思路比较简单：要将最新使用/插入的缓存放到最前——最晚被淘汰，这种就是要调整节点顺序，所以是要使用链表的，使用数组的复杂度会变成 O(N^2)。另外，get 的复杂度要是 O(1) 就需要使用到哈希表。

链表选择双向链表，因为在删除的时候，只知道当前node，无法做到前边节点连接后边节点。双向链表构造的时候，除了头，还有个尾，为的是能在O(1) 复杂度淘汰掉的尾部的元素。

只要认真点写，双向链表的操作甚至比单链表的操作更简单。

从 LRU 到 ZSET

LRU的题目很容易让人联想到 Redis 的 ZSET ，它是一种有序集合，支持按 score 排序的操作。我们上边实现 LRU 的一些操作都在 ZSET 中有对应的指令：

• get(key)：ZSCORE，当然这里只能判断缓存在不在，而缓存内容则无法直接通过 ZSET 存储
• put(key, value)：ZADD，同样的，需要有另外的 Redis key 来存储对应缓存
• 淘汰超过容量且最近使用最少的缓存：通过 ZCARD 指令获得集合中的元素数量（基数 cardinality），如果超过了容量，则通过 ZPOPMIN 指令将最小分值元素给删除掉

Redis ZSET 的实现原理

ZSET 看上去有跟 LRU 类似的功能，那他是不是也是类似的实现呢？

我们考虑这个问题，得考虑下 ZSET 比 LRU 还有什么额外的功能：ZSET 是一个有序集，其插入不仅仅是插入到头部，而是可以有序地插入；可以通过 ZRANGE 指令按照 score 返回获取元素；也可以按照score范围删除元素。

可见，ZSET 的功能比 LRU 是要更多的——排序，仅靠哈希表和双向链表是无法完成排序的，即使保持有序，双向链表也不能通过二分查找快速定位到一个元素的位置

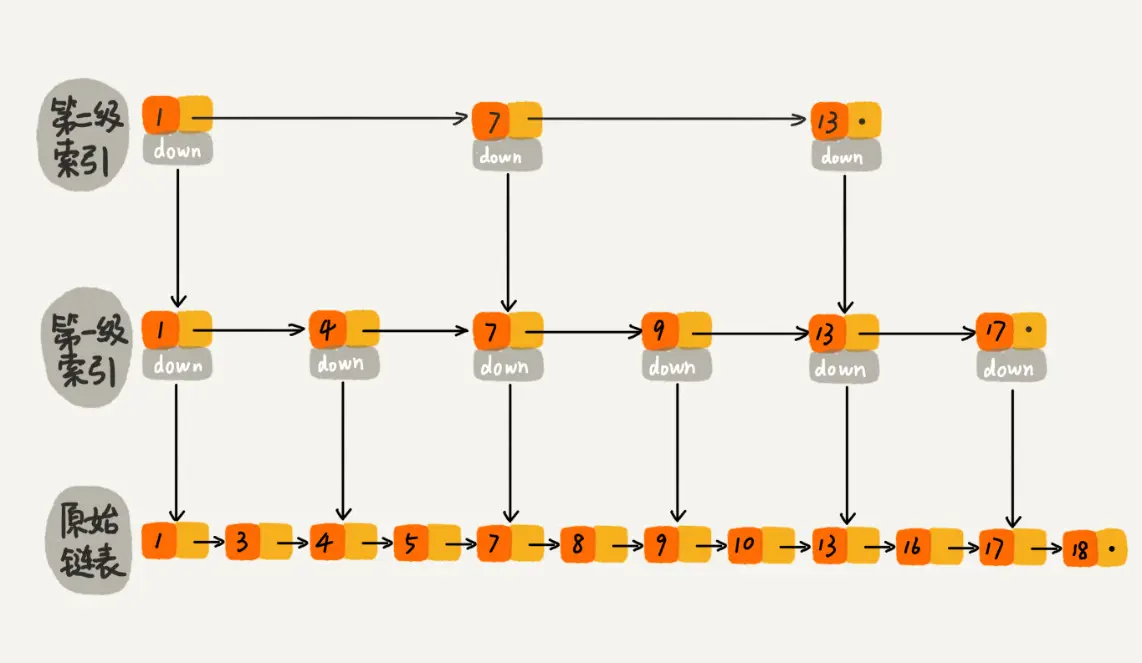
因此，ZSET的实现，还使用了跳表。跳表是一种随机化的数据结构，支持快速的插入、删除和查找操作。跳表的时间复杂度为 O(log N)，与平衡二叉树类似，但实现更简单。跳表通过多级链表来实现，每一级链表包含一部分元素，元素在不同级别链表中的概率是固定的。

跳表的原理比较简单，就是使用多个链表作为多级索引，每一级索引都是有序的。通过设置多集索引，可以将查找对应 Score 的时间控制在跟二分查找类似的程度。

乍一看好像跳表的难点不在于查找、删除，更在于插入时索引的构建。其实这里索引的构建，实现时有一个技巧：假如跳表每一层的晋升概率是 1/2，那么在这个元素插入的时候，就通过随机数和 1/2、1/4、1/8 …的比较，来判断，这个值是否会作为第1级、第2级、第3级…的索引。

有序集合 —— C++ map

C++ 的 map 是一个关联容器，它使用红黑树（Red-Black Tree）来实现。红黑树是一种自平衡二叉搜索树，能够保证插入、删除和查找操作的时间复杂度为 O(log n)。

当使用迭代器遍历 std::map 时，迭代器会按照键的升序（从小到大）遍历所有元素 key，同样的还有 std::set 也是使用红黑树实现的，是按照值的从小到大遍历。】

可以看到，跳表和红黑树都是用于实现有序集合的数据结构，他们的空间复杂度都是 O(n)。跳表实现起来更加简单直观，而红黑树更复杂，但是红黑树能够该保证最坏情况下其查找、插入、删除的算法复杂度也是 O(log n)，而跳表的平均复杂度是 O(log n)，在极端情况下，可能达到 O(n)。

无序集合——Go 中 map 的实现

Golang 的 map 的实现和 C++ 的 map 不同，但和 C++ 的 unordered_map 类似，都是哈希表的实现。

基于哈希表实现，可以提供了平均 O(1) 时间复杂度的查找、插入和删除操作，但是不能保证顺序。

Go map 的实现中，会利用 buckets 数组来键对应 hash 值。

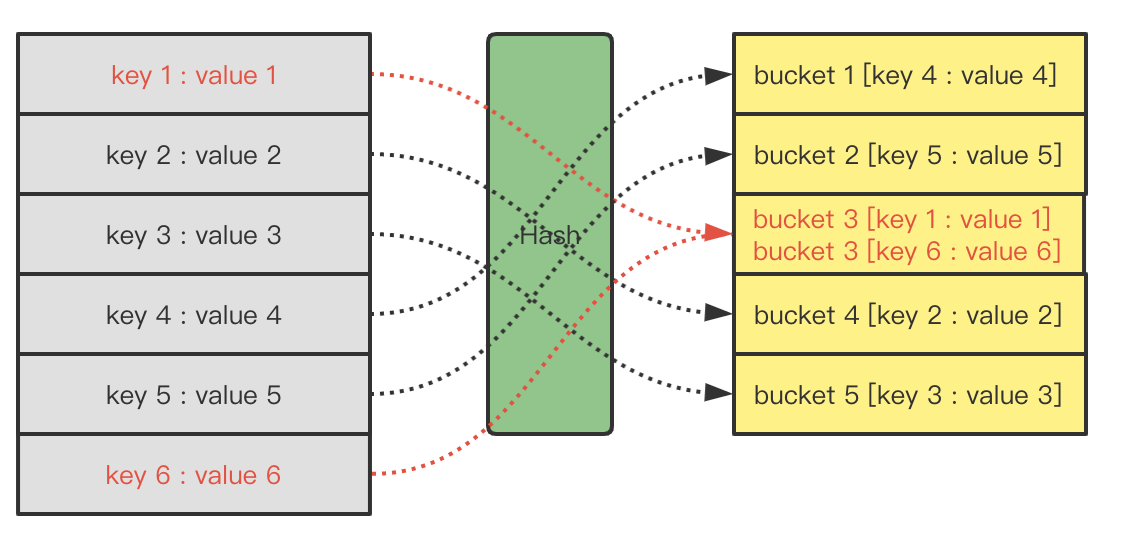
如果发生 hash 冲突，buckets 可以链接多个键值对——拉链法。当一个bucket中键值对数量超过限制，就会通过 evacuate() 函数进行扩容。

按插入顺序 —— Python dict

在 Python 3.7 之前，遍历**字典 dict**中的 key 是没有保证顺序的，即使你程序每次输出都一样，只要是没有写入规范的，都是不可以依赖的行为。

而在 Python 3.7 及之后的版本中保证插入顺序的行为已经被正式纳入语言规范。

the insertion-order preservation nature of dict objects has been declared to be an official part of the Python language spec.

跟 Go 和 C++ 中的 map 遍历都不太一样，他是保持插入顺序，是通过内部三个数组来实现的：

1. 键值对数组：存储实际的键和值
2. 哈希表数组：存储哈希值和指向键值对数组的索引
3. 插入顺序数组：按照插入顺序存储键值对数组的索引

这样能保证可以按照插入顺序遍历。但是这里如果涉及到删除索引，可能复杂度会高一些，但是Python也有做了一些标记删除、延迟处理等一些优化。